Materi matematika FPB dan KPK merupakan dasar penting dalam pemahaman konsep faktor dan kelipatan. Memahami konsep FPB (Faktor Persekutuan Terbesar) dan KPK (Kelipatan Persekutuan Terkecil) sangat krusial dalam berbagai aplikasi matematika, mulai dari menyelesaikan soal cerita hingga mempersiapkan diri untuk materi matematika yang lebih kompleks. Pada materi ini, kita akan menjelajahi definisi, metode pencarian, hubungan, dan penerapan FPB dan KPK dalam konteks matematika.
Materi ini akan membahas secara detail tentang cara menentukan FPB dan KPK menggunakan metode faktorisasi prima dan pembagian berulang. Kita juga akan melihat contoh-contoh penerapannya dalam kehidupan sehari-hari, dan bagaimana konsep ini terhubung dengan materi matematika lainnya, seperti pecahan dan persamaan linier. Selain itu, akan disajikan ilustrasi visual untuk mempermudah pemahaman konsep-konsep yang abstrak.
Definisi FPB dan KPK: Materi Matematika Fpb Dan Kpk
Faktor Persekutuan Terbesar (FPB) dan Kelipatan Persekutuan Terkecil (KPK) merupakan konsep penting dalam matematika yang sering diaplikasikan dalam kehidupan sehari-hari. Memahami konsep ini akan mempermudah pemecahan masalah yang berkaitan dengan pembagian dan pengelompokan.
Pengertian FPB
Faktor Persekutuan Terbesar (FPB) adalah bilangan bulat positif terbesar yang dapat membagi habis dua atau lebih bilangan bulat positif. FPB dapat diartikan sebagai bilangan terbesar yang merupakan faktor dari dua atau lebih bilangan tersebut.
Contoh: Tentukan FPB dari 12 dan 18. Faktor dari 12 adalah 1, 2, 3, 4, 6, dan 12. Faktor dari 18 adalah 1, 2, 3, 6, 9, dan 18. Faktor persekutuan dari 12 dan 18 adalah 1, 2, 3, dan 6. FPB dari 12 dan 18 adalah 6.
Pengertian KPK
Kelipatan Persekutuan Terkecil (KPK) adalah bilangan bulat positif terkecil yang merupakan kelipatan dari dua atau lebih bilangan bulat positif. KPK dapat diartikan sebagai bilangan terkecil yang merupakan kelipatan dari dua atau lebih bilangan tersebut.
Contoh: Tentukan KPK dari 4 dan 6. Kelipatan 4 adalah 4, 8, 12, 16, 20, dan seterusnya. Kelipatan 6 adalah 6, 12, 18, 24, dan seterusnya. Kelipatan persekutuan dari 4 dan 6 adalah 12, 24, dan seterusnya. KPK dari 4 dan 6 adalah 12.
Penerapan FPB dalam Kehidupan Sehari-hari
FPB sering diterapkan dalam permasalahan pembagian dan pengelompokan. Misalnya, dalam membagi kue menjadi beberapa bagian yang sama besar, atau dalam membagi barang ke dalam kelompok-kelompok dengan jumlah yang sama.
- Membagi kue ulang tahun ke beberapa orang secara merata.
- Menyusun buku di rak dengan jumlah yang sama.
Penerapan KPK dalam Kehidupan Sehari-hari
KPK sering diterapkan dalam permasalahan yang berkaitan dengan siklus atau kejadian yang berulang. Misalnya, dalam menentukan waktu pertemuan dua orang atau lebih.
- Menentukan waktu pertemuan dua orang yang memiliki jadwal berbeda.
- Menentukan waktu keberangkatan kereta api atau bus dengan jadwal yang berbeda.
Perbandingan FPB dan KPK
| Aspek | FPB | KPK |
|---|---|---|
| Definisi | Bilangan bulat positif terbesar yang dapat membagi habis dua atau lebih bilangan. | Bilangan bulat positif terkecil yang merupakan kelipatan dari dua atau lebih bilangan. |
| Tujuan | Menentukan faktor persekutuan terbesar. | Menentukan kelipatan persekutuan terkecil. |
| Penerapan | Pembagian, pengelompokan. | Siklus, kejadian berulang. |
Metode Pencarian FPB
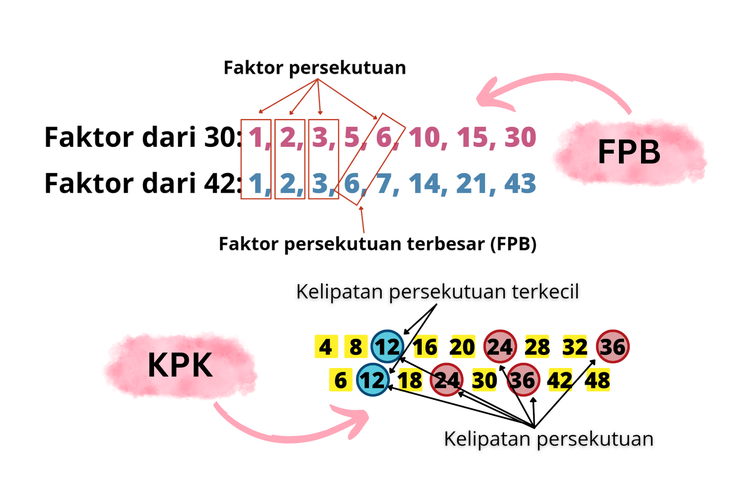
Berikut ini akan dibahas dua metode efektif dalam menemukan Faktor Persekutuan Terbesar (FPB) dari beberapa bilangan. Kedua metode ini menawarkan pendekatan berbeda namun sama-sama valid dalam menghasilkan jawaban yang akurat.
Metode Faktorisasi Prima
Metode faktorisasi prima melibatkan penguraian setiap bilangan menjadi faktor-faktor primanya. Faktor prima adalah bilangan bulat yang hanya habis dibagi oleh 1 dan dirinya sendiri. FPB dari beberapa bilangan adalah hasil kali dari faktor prima yang paling kecil yang terdapat pada semua bilangan tersebut.
- Identifikasi Faktor Prima: Temukan faktor prima dari masing-masing bilangan yang dicari FPB-nya.
- Pilih Faktor Prima yang Sama: Cari faktor prima yang sama pada semua bilangan tersebut.
- Tentukan Pangkat Terkecil: Tentukan pangkat terkecil dari faktor prima yang sama yang ditemukan pada langkah sebelumnya.
- Kalikan Faktor Prima: Kalikan semua faktor prima yang sama dengan pangkat terkecil yang ditemukan pada langkah sebelumnya.
Contoh Metode Faktorisasi Prima
Cari FPB dari 12 dan 18.
- Faktorisasi prima dari 12 adalah 22 × 3.
- Faktorisasi prima dari 18 adalah 2 × 3 2.
- Faktor prima yang sama adalah 2 dan 3.
- Pangkat terkecil dari 2 adalah 2 1 dan pangkat terkecil dari 3 adalah 3 1.
- FPB dari 12 dan 18 adalah 2 1 × 3 1 = 6.
Metode Pembagian Berulang
Metode pembagian berulang merupakan pendekatan sistematis yang berfokus pada pembagian berulang dari bilangan-bilangan yang dicari FPB-nya. Metode ini menggunakan pembagian berulang hingga didapatkan sisa nol.
- Pilih Bilangan Terkecil: Pilih bilangan terkecil dari bilangan-bilangan yang dicari FPB-nya.
- Bagi Bilangan Terbesar dengan Bilangan Terkecil: Bagi bilangan terbesar dengan bilangan terkecil. Catat hasil bagi dan sisanya.
- Gantikan Bilangan Terbesar dengan Sisa: Gantikan bilangan terbesar dengan sisa pembagian sebelumnya.
- Ulangi Langkah-langkah di atas: Ulangi langkah-langkah pembagian sampai didapatkan sisa pembagian nol. FPB adalah bilangan terakhir yang membagi habis.
Contoh Metode Pembagian Berulang
Cari FPB dari 24 dan 36.
- Bagi 36 dengan 24: 36 ÷ 24 = 1 sisa 12.
- Gantikan 36 dengan
12. Bagi 24 dengan 12
24 ÷ 12 = 2 sisa 0.
- Karena sisa pembagian terakhir adalah nol, maka FPB dari 24 dan 36 adalah 12.
Perbandingan Metode
| Metode | Langkah-langkah |
|---|---|
| Faktorisasi Prima |
|
| Pembagian Berulang |
|
Metode Pencarian KPK

Setelah memahami konsep FPB, sekarang kita akan beralih ke KPK (Kelipatan Persekutuan Terkecil). KPK merupakan bilangan terkecil yang merupakan kelipatan dari dua atau lebih bilangan. Memahami cara mencari KPK sangatlah penting dalam matematika, karena sering digunakan dalam berbagai penerapan, seperti dalam perhitungan pecahan atau dalam menyelesaikan masalah sehari-hari.
Metode Faktorisasi Prima
Metode faktorisasi prima adalah salah satu cara efektif untuk mencari KPK. Metode ini berfokus pada menguraikan bilangan-bilangan menjadi faktor-faktor primanya. Langkah-langkahnya adalah sebagai berikut:
- Faktorisasi prima masing-masing bilangan.
- Ambil semua faktor prima yang muncul pada setiap faktorisasi.
- Tentukan pangkat tertinggi masing-masing faktor prima yang ditemukan.
- Kalikan semua faktor prima berpangkat tertinggi tersebut.
Metode Kelipatan
Metode kelipatan melibatkan penentuan kelipatan-kelipatan dari masing-masing bilangan. Langkah-langkahnya adalah sebagai berikut:
- Tentukan kelipatan-kelipatan dari masing-masing bilangan.
- Identifikasi kelipatan persekutuan dari bilangan-bilangan tersebut.
- Pilih kelipatan persekutuan terkecil.
Contoh Menggunakan Faktorisasi Prima
Misalnya, kita ingin mencari KPK dari 12 dan 18.
- Faktorisasi prima dari 12 adalah 22 × 3.
- Faktorisasi prima dari 18 adalah 2 × 3 2.
- Faktor prima yang muncul adalah 2 dan 3. Pangkat tertinggi 2 adalah 2 2, dan pangkat tertinggi 3 adalah 3 2.
- KPK(12, 18) = 2 2 × 3 2 = 4 × 9 = 36.
Contoh Menggunakan Metode Kelipatan
Misalnya, kita ingin mencari KPK dari 4 dan 6.
- Kelipatan 4: 4, 8, 12, 16, 20, …
- Kelipatan 6: 6, 12, 18, 24, …
- Kelipatan persekutuan: 12, 24, …
- Kelipatan persekutuan terkecil adalah 12.
Perbandingan Kedua Metode
| Langkah | Metode Faktorisasi Prima | Metode Kelipatan |
|---|---|---|
| Menentukan faktorisasi prima | Ya | Tidak |
| Menentukan pangkat tertinggi | Ya | Tidak |
| Mencari kelipatan | Tidak | Ya |
| Memilih kelipatan persekutuan terkecil | Tidak | Ya |
| Efisiensi | Biasanya lebih efisien untuk bilangan yang lebih besar | Efisien untuk bilangan yang relatif kecil |
Hubungan FPB dan KPK

FPB dan KPK merupakan dua konsep penting dalam matematika yang berkaitan erat. Memahami hubungan antara keduanya akan memudahkan dalam menyelesaikan berbagai soal. Berikut penjelasan mengenai hubungan tersebut.
Hubungan antara FPB dan KPK dari Dua Bilangan
Terdapat hubungan khusus antara FPB (Faktor Persekutuan Terbesar) dan KPK (Kelipatan Persekutuan Terkecil) dari dua bilangan. Hubungan ini sangat berguna dalam menyelesaikan soal-soal yang melibatkan FPB dan KPK.
Contoh Soal yang Menunjukkan Hubungan FPB dan KPK
Misalnya, kita ingin mencari FPB dan KPK dari 12 dan 18. FPB(12, 18) = 6 dan KPK(12, 18) = 36. Perhatikan bahwa perkalian FPB dan KPK sama dengan perkalian kedua bilangan tersebut.
Perhitungan: (6 x 36) = 216 dan (12 x 18) = 216. Hal ini menunjukkan bahwa 216 sama dengan perkalian dari 12 dan 18.
Rumus yang Menjelaskan Hubungan FPB dan KPK
FPB(a, b) × KPK(a, b) = a × b
Rumus di atas menjelaskan hubungan antara FPB dan KPK dari dua bilangan, a dan b. Perkalian dari FPB dan KPK sama dengan perkalian dari kedua bilangan tersebut.
Mencari KPK jika FPB-nya Sudah Diketahui
Jika kita sudah mengetahui FPB dari dua bilangan, kita dapat mencari KPK-nya dengan menggunakan rumus di atas. Kita hanya perlu membagi perkalian kedua bilangan dengan FPB-nya.
Contoh: Jika FPB(a, b) = 6 dan a × b = 216, maka KPK(a, b) = 216 / 6 = 36.
Bagan Alir untuk Mencari FPB dan KPK, Materi matematika fpb dan kpk
Berikut bagan alir yang merangkum langkah-langkah mencari FPB dan KPK dari dua bilangan:
- Cari faktor-faktor prima dari masing-masing bilangan.
- Tentukan faktor prima yang sama dan pangkat terkecil untuk mencari FPB.
- Tentukan faktor prima dari kedua bilangan dan pangkat terbesar untuk mencari KPK.
- Jika FPB diketahui, gunakan rumus FPB(a, b) × KPK(a, b) = a × b untuk mencari KPK.
Contoh Soal dan Pembahasan
Untuk memperdalam pemahaman tentang FPB dan KPK, mari kita bahas beberapa contoh soal dan pembahasannya. Contoh-contoh ini akan membantu Anda mengaplikasikan konsep FPB dan KPK dalam berbagai situasi.
Contoh Soal FPB
Berikut lima contoh soal FPB dengan penyelesaiannya:
- Carilah FPB dari 12 dan 18.
Penyelesaian: Faktor dari 12: 1, 2, 3, 4, 6,12. Faktor dari 18
1, 2, 3, 6, 9, 18. Faktor persekutuan dari 12 dan 18 adalah 1, 2, 3, dan 6. FPB dari 12 dan 18 adalah 6.
- Carilah FPB dari 24, 36, dan 48.
Penyelesaian: Faktor dari 24: 1, 2, 3, 4, 6, 8, 12,24. Faktor dari 36
1, 2, 3, 4, 6, 9, 12, 18,
36. Faktor dari 48
1, 2, 3, 4, 6, 8, 12, 16, 24, 48. Faktor persekutuan dari 24, 36, dan 48 adalah 1, 2, 3, 4, 6, dan 12. FPB dari 24, 36, dan 48 adalah 12.
- Carilah FPB dari 15 dan 25.
Penyelesaian: Faktor dari 15: 1, 3, 5,15. Faktor dari 25
1, 5, 25. Faktor persekutuan dari 15 dan 25 adalah 1 dan 5. FPB dari 15 dan 25 adalah 5.
- Carilah FPB dari 30 dan 45.
Penyelesaian: Faktor dari 30: 1, 2, 3, 5, 6, 10, 15,30. Faktor dari 45
1, 3, 5, 9, 15, 45. Faktor persekutuan dari 30 dan 45 adalah 1, 3, 5, dan 15. FPB dari 30 dan 45 adalah 15.
- Carilah FPB dari 27 dan 45.
Penyelesaian: Faktor dari 27: 1, 3, 9,27. Faktor dari 45
1, 3, 5, 9, 15, 45. Faktor persekutuan dari 27 dan 45 adalah 1, 3, dan 9. FPB dari 27 dan 45 adalah 9.
Contoh Soal KPK
Berikut lima contoh soal KPK dengan penyelesaiannya:
- Carilah KPK dari 4 dan 6.
Penyelesaian: Kelipatan 4: 4, 8, 12, 16, 20, … Kelipatan 6: 6, 12, 18, 24, 30, … Kelipatan persekutuan terkecil dari 4 dan 6 adalah 12. KPK dari 4 dan 6 adalah 12. - Carilah KPK dari 8 dan 12.
Penyelesaian: Kelipatan 8: 8, 16, 24, 32, … Kelipatan 12: 12, 24, 36, 48, … Kelipatan persekutuan terkecil dari 8 dan 12 adalah 24. KPK dari 8 dan 12 adalah 24. - Carilah KPK dari 10 dan 15.
Penyelesaian: Kelipatan 10: 10, 20, 30, 40, … Kelipatan 15: 15, 30, 45, 60, … Kelipatan persekutuan terkecil dari 10 dan 15 adalah 30. KPK dari 10 dan 15 adalah 30. - Carilah KPK dari 12, 18, dan 24.
Penyelesaian: Kelipatan 12: 12, 24, 36, 48, … Kelipatan 18: 18, 36, 54, 72, … Kelipatan 24: 24, 48, 72, 96, … Kelipatan persekutuan terkecil dari 12, 18, dan 24 adalah 72. KPK dari 12, 18, dan 24 adalah 72. - Carilah KPK dari 9 dan 21.
Penyelesaian: Kelipatan 9: 9, 18, 27, 36, 45, 54, 63, … Kelipatan 21: 21, 42, 63, 84, … Kelipatan persekutuan terkecil dari 9 dan 21 adalah 63. KPK dari 9 dan 21 adalah 63.
Contoh Soal Cerita
Berikut contoh soal cerita yang melibatkan FPB dan KPK:
Ani memiliki 24 permen jeruk dan 36 permen stroberi. Ani ingin membagi permen tersebut ke dalam beberapa kantong dengan jumlah permen jeruk dan stroberi yang sama di setiap kantong. Berapa kantong terbanyak yang dapat dibuat Ani?
Penyelesaian:
Soal ini meminta FPB dari 24 dan 36.
FPB dari 24 dan 36 adalah 12.
Jadi, Ani dapat membuat 12 kantong.
Penerapan dalam Matematika Lanjut
Konsep Faktor Persekutuan Terbesar (FPB) dan Kelipatan Persekutuan Terkecil (KPK) tidak hanya terbatas pada operasi dasar bilangan bulat. Kedua konsep ini berperan penting dalam pemahaman dan penyelesaian berbagai materi matematika yang lebih kompleks.
Penerapan pada Materi Pecahan dan Operasi Bilangan
FPB dan KPK sangat berguna dalam menyederhanakan pecahan. Misalnya, untuk menyederhanakan pecahan 12/18, kita dapat mencari FPB dari 12 dan 18, yaitu 6. Kemudian, membagi pembilang dan penyebut dengan FPB tersebut akan menghasilkan pecahan yang setara dan lebih sederhana, yaitu 2/3. Selain itu, KPK juga berperan dalam menyamakan penyebut saat melakukan penjumlahan atau pengurangan pecahan.
Penerapan pada Materi Persamaan Linier
Dalam persamaan linier, FPB dan KPK dapat membantu dalam mencari solusi yang tepat. Misalnya, dalam mencari penyelesaian persamaan linier dengan variabel yang melibatkan pecahan, menyamakan penyebut menggunakan KPK akan memudahkan proses penyederhanaan dan penyelesaian.
Peran FPB dan KPK dalam Menyelesaikan Masalah Matematika Kompleks
Dalam berbagai soal cerita matematika yang kompleks, seringkali diperlukan pemahaman tentang FPB dan KPK untuk menemukan solusi yang tepat. Misalnya, soal yang berkaitan dengan pembagian barang secara merata, penentuan jadwal yang berulang, atau masalah yang melibatkan beberapa variabel yang terkait dengan kelipatan atau faktor. Dengan menguasai FPB dan KPK, penyelesaian masalah tersebut akan lebih terstruktur dan efisien.
Ringkasan Materi Terkait FPB dan KPK
- FPB digunakan untuk menyederhanakan pecahan.
- KPK digunakan untuk menyamakan penyebut dalam operasi pecahan.
- FPB dan KPK dapat membantu dalam mencari solusi persamaan linier yang melibatkan pecahan.
- Pemahaman FPB dan KPK esensial dalam menyelesaikan masalah matematika kompleks yang berkaitan dengan kelipatan atau faktor.
Ilustrasi Visual
Memahami konsep FPB dan KPK akan lebih mudah dengan bantuan ilustrasi visual. Visualisasi ini dapat membantu dalam memahami hubungan antar konsep dan memudahkan dalam penerapannya.
Ilustrasi Konsep FPB
Konsep FPB dapat diilustrasikan dengan diagram Venn. Misalnya, kita ingin mencari FPB dari 12 dan 18. Kita tuliskan faktor-faktor dari masing-masing bilangan. Faktor 12 adalah 1, 2, 3, 4, 6, dan 12. Faktor 18 adalah 1, 2, 3, 6, 9, dan 18.
Daerah irisan (bagian yang sama) dari kedua diagram Venn merepresentasikan faktor persekutuan terbesar, yaitu 6.
Ilustrasi Konsep KPK
Konsep KPK dapat diilustrasikan dengan diagram garis bilangan. Misalnya, kita ingin mencari KPK dari 4 dan 6. Kelipatan 4 adalah 4, 8, 12, 16, 20, dan seterusnya. Kelipatan 6 adalah 6, 12, 18, 24, dan seterusnya. Bilangan terkecil yang ada pada kedua garis bilangan adalah 12, sehingga KPK dari 4 dan 6 adalah 12.
Ilustrasi Hubungan FPB dan KPK
FPB dan KPK memiliki hubungan yang erat. Misalnya, untuk bilangan 12 dan 18, FPB-nya adalah 6 dan KPK-nya adalah 36. Jika kita kalikan FPB dan KPK, hasilnya sama dengan perkalian kedua bilangan tersebut. Dengan kata lain, (FPB(12, 18)) × (KPK(12, 18)) = 12 × 18 = 216.
Ilustrasi Faktorisasi Prima untuk Mencari FPB dan KPK
Faktorisasi prima dapat digunakan untuk menemukan FPB dan KPK dengan lebih sistematis. Misalnya, untuk mencari FPB dan KPK dari 24 dan 36. Faktorisasi prima dari 24 adalah 2 3 × 3, dan faktorisasi prima dari 36 adalah 2 2 × 3 2. Untuk FPB, kita ambil faktor-faktor prima yang sama dengan pangkat terkecil. FPB(24, 36) = 2 2 × 3 = 12.
Untuk KPK, kita ambil faktor-faktor prima yang ada dengan pangkat terbesar. KPK(24, 36) = 2 3 × 3 2 = 72.
Ilustrasi Contoh Soal FPB dan KPK
Berikut ilustrasi sederhana untuk contoh soal FPB dan KPK:
- Contoh 1: Mencari FPB dari 15 dan 25. Gambar dua lingkaran yang mewakili faktor 15 dan 25. Faktor persekutuan terbesar adalah 5.
- Contoh 2: Mencari KPK dari 4 dan 6. Tuliskan beberapa kelipatan 4 dan 6. Kelipatan persekutuan terkecil adalah 12. Gambar garis bilangan yang menunjukkan kelipatan tersebut.
Penutupan
Kesimpulannya, materi FPB dan KPK ini menawarkan pemahaman mendalam tentang faktor dan kelipatan. Dengan menguasai konsep dan metode yang dibahas, diharapkan pembaca dapat menyelesaikan berbagai soal matematika yang berkaitan dengan FPB dan KPK, serta menerapkannya dalam kehidupan sehari-hari. Semoga materi ini bermanfaat dan memperkaya pemahaman matematika Anda.